MTH306Y
- MAPLE figures
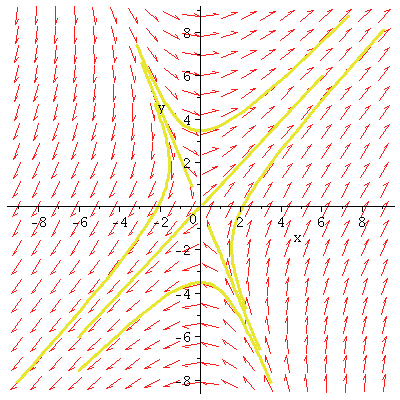
Phase
Portraits for Linear Systems with Real Eigenvalues (Section 3.3)
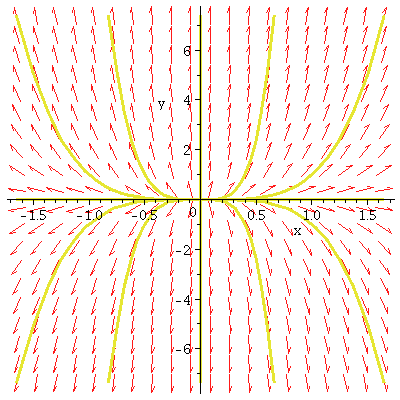
(a) A "simple" sink
dx/dt=-x
dy/dt=-4y
eigenvalue: -1 straight-line solutions on y=0
eigenvalue: -4 straight-line
solutions on x=0
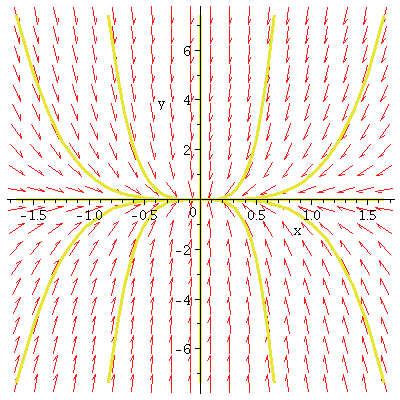
(b) A more general sink
dx/dt=-5x-2y
dy/dt=-x-4y
eigenvalue: -3 straight-line solutions on y=-x
eigenvalue: -6 straight-line solutions on
y=x/2
(c) A "simple" source
dx/dt=x
dy/dt=4y
eigenvalue: 1 straight-line solutions on y=0
eigenvalue: 4 straight-line
solutions on x=0
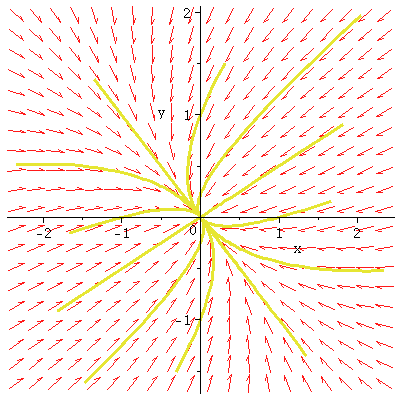
(d) A more general source
dx/dt=5x+2y
dy/dt=x+4y
eigenvalue: 3 straight-line solutions on y=-x
eigenvalue: 6 straight-line solutions on
y=x/2

(e) A "simple" saddle
dx/dt=-2x
dy/dt=4y
eigenvalue: -2 straight-line solutions on y=0
eigenvalue: 4 straight-line
solutions on x=0
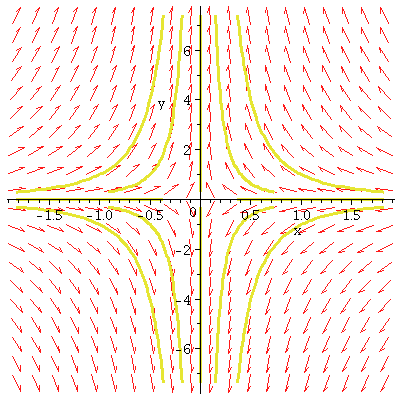
(f) A more general saddle
dx/dt=5x+4y
dy/dt=9x
eigenvalue: -4 straight-line solutions on y=-9x/4
eigenvalue: 9 straight-line
solutions on y=x
Vector
Fields (Section 2.2)
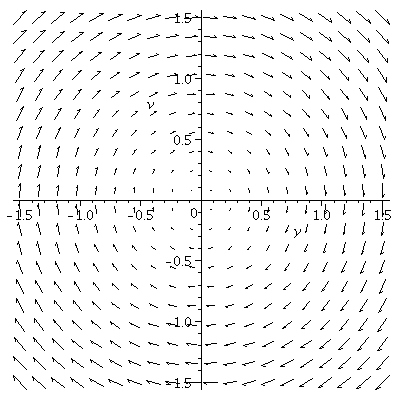
(a) Vector field for
dy/dt=v
dv/dt=-y
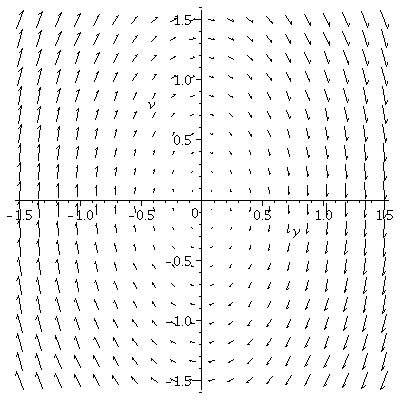
(b) Vector field for
dy/dt=v
dv/dt=-3y
(c) Vector field for
dx/dt=-x
dy/dt=-y

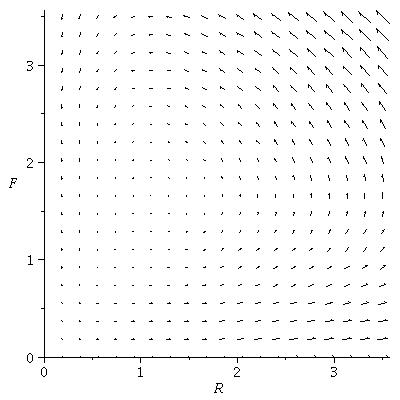
(d) Vector field for
dR/dt=2R-1.2RF
dF/dt=-F+0.9RF
Slope
Fields (Section 1.3)
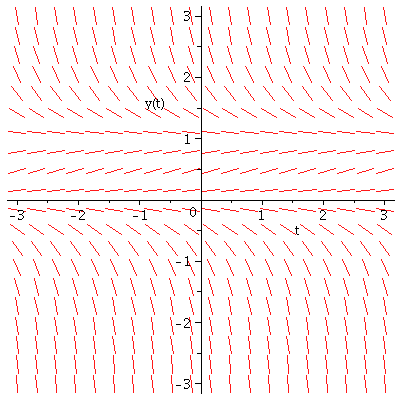
(a) Slope field for y'=y-t
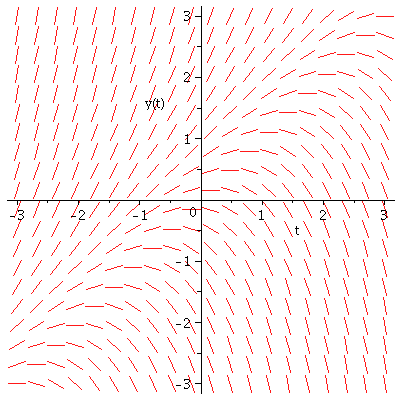
(b) Slope field for y'=t2
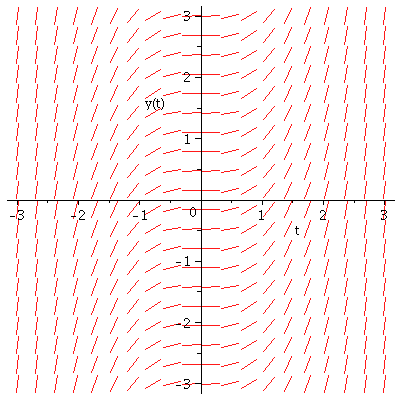
(c) Slope field for y'=y(1-y)
Back
to
course
web page












