page3
|
COMPACT, a tutorial by Scott W. Williams |
||
|
page 1: |
page 2: |
|
|
page3: |
page4: |
page5: |
Disjoint or non-intersecting closed sets one of which is compact in a (Hausdorff) topological space can be expanded to disjoint open sets - this is called separating them.
The distance, in the plane, between the disjoint
closed sets, graphs of y=0 and xy=1
is 0. Neither of
these sets is compact and ![]() is necessary for this process. Suppose H and K are disjoint closed
sets of a space X. If we can not expand these two to disjoint
open sets then there must be some kind of "hole"
present: Consider the Tychonov Plank, the space X is the product
is necessary for this process. Suppose H and K are disjoint closed
sets of a space X. If we can not expand these two to disjoint
open sets then there must be some kind of "hole"
present: Consider the Tychonov Plank, the space X is the product
![]() with the
upper right hand corner removed; i.e.,
with the
upper right hand corner removed; i.e., ![]() .
The closed sets are the top A=
.
The closed sets are the top A=![]() and the right hand side B=
and the right hand side B=![]() .
.
![]()

{Key to the proof is that the hole at the end of A (see 1.4.5) is so far away that any open set containing B contains countable sequences converging to A; i.e., limit points belonging to A. Thus, there can be no disjoint open sets containing A and B.}
Even stronger (superficially) than "expansion of disjoint closed sets to disjoint open sets" is "separation of closed sets by a continuous function."
3.1. THEOREM. If A
and B are disjoint
closed subsets of a compact space X there is a continuous f:X![]() [0,1] such that f(A)=0 and f(B)=1.
[0,1] such that f(A)=0 and f(B)=1.
Let us return to products: Fréchet was the first to define a finite product of topological spaces [Fréchet1910]. That the product of two compact spaces are compact is intuitively clear: A "hole" in the product of X and Y ought to imply it in a factor. Induction shows "two" can be replaced by "finitely many." But what about "infinitely many?"
In 1923 Tietze first gave the definition of a topology, called the box topology, on a product of infinitely many spaces to be that which is generated by the product of open sets [Tietze1923]:
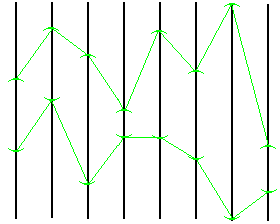
This definition is the "right" way to define product in many areas of mathematics (example, in Algebra). However, even the product of countably many two element sets is not compact.
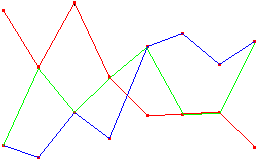
Further, an important old (at least the 1960's and prehaps the 1920's) and major unsolved problem [Williams1984] in topology asks,
Does the product (with the box topology) of countably many copies of [0,1] satisfy the conclusion of Theorem 3.1 ?
The answer to large products in general is
"NO!";
i.e., there are A
and B are disjoint
closed subsets of the product of uncountably many copies of [0,1] for which no continuous
function f:X![]() [0,1] satisfies both f(A)=0 and f(B)=1
[Lawrence1994].
[0,1] satisfies both f(A)=0 and f(B)=1
[Lawrence1994].
Clearly, Tietze's topology is not good for proving theorems in infinite products (e.g., the preservation of compactness, connectedness, metric etc.), and thus we use a product topology [Tychonov1930] which, like compactness, extends finite delicately - the topology is generated by a product of open sets which, only finitely often, may be different from the entire factor:
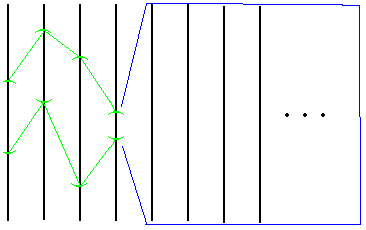
This guarantees that a hole in the product must come from a hole in at least one factor and the standard:
3.2. THEOREM. The product of arbitrarily many compact spaces are compact.
![]()
|
page 1: the beginnings |
page 2: a special example |
page3: functional separation |
|
|
page4: the universe in a box |
page5: open covers |
||